Центр давления
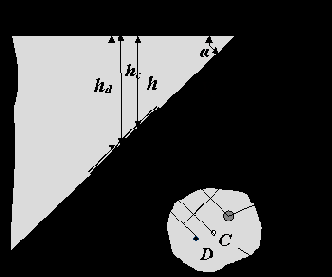
Распределённую нагрузку, действующую на наклонную стенку, заменим сконцентрированной. Для этого найдём на наклонной стенке положение точки D, в которой приложена равнодействующая силы давления. Точку, в которой приложена эта сила, называют центром давления. Как уже неоднократно рассматривалось, давление, действующее в любой точке, в соответствии с основным уравнением гидростатики складывается из двух частей: внешнего давления P0, передающегося всем точкам жидкости одинаково, и давления столба жидкости P, определяемого глубиной погружения этой точки.
Давление P0 передаётся всем точкам площадки одинаково. Следовательно, равнодействующая Fвн
этого давления будет приложена в центре тяжести площадки S. При этом надо учитывать, что в большинстве случаев это давление действует и со стороны жидкости и с наружной стороны стенки.
 |
Давление
P увеличивается с увеличением глубины. При этом величина равнодействующей этой силы Fизб известна и равна
 а точку её приложения необходимо определить. |

где YD - координата точки приложения силы Fизб,
Y – текущая глубина.
Учтём, что, если hc выразить как координату точки C по оси Y, то Fизб примет вид:

Заменив в этом выражении Fизб и YD интегралом, в соответствии с упомянутым уравнением механики, будем иметь:

Отсюда выразим YD:

Интеграл в числителе дроби является статическим моментом инерции площади S относительно оси 0X и обычно обозначается Jx

Из теоретической механики известно, что статический момент площади относительно оси вращения равен сумме собственного момента инерции (момента инерции этой площади относительно оси проходящей через её центр тяжести и параллельной первой оси) и произведению этой площади на квадрат расстояния от оси вращения до центра её тяжести

С учётом последнего определения YD окончательно можно выразить в виде:

Таким образом, разница в положениях ?Y (глубинах) центра тяжести площадки (т. C) и центра давления (т. D) составляет

В итоге можно сделать следующие выводы. Если внешнее давление действует на стенку с обеих сторон, то найденная точка D будет являться центром давления. Если внешнее давление со стороны жидкости выше давления с противоположной стороны (например, атмосферного), то центр давления находится по правилам механики как точка приложения равнодействующей двух сил: силы, создаваемой внешним давлением, и силы, создаваемой весом жидкости. При этом, чем больше внешнее давление, тем ближе располагается центр давления к центру тяжести.
В гидроприводе технологического оборудования внешние давления в десятки и сотни раз превышают давления, вызванные высотой столба жидкости. Поэтому в расчётах гидравлических машин и аппаратов положение центров давления принимаются совпадающими с центрами тяжести.